Inversión de intervalos: concepto
Invertir un intervalo consiste en cambiar el orden de las notas, de tal forma que la nota aguda pasa a ser la grave, y viceversa.
Intervalos simples:
¿Cómo se invierten?
Se procede, o bien subiendo una octava la nota grave del intervalo, o bien bajando una octava la nota aguda.
Ejemplo:
 Subiendo el “fa” una octava, se invierte el intervalo: la tercera (mayor) pasa a sexta (menor).
Subiendo el “fa” una octava, se invierte el intervalo: la tercera (mayor) pasa a sexta (menor).
Transformaciones que sufren al ser invertidos:
| Numérica | Especie |
|---|---|
| · La 2ª pasa a 7ª · La 3ª pasa a 6ª · La 4ª pasa a 5ª · La 5ª pasa a 4ª · La 6ª pasa a 3ª · La 7ª pasa a 2ª · La 8ª a unísono o 1ª |
· Mayor pasa a Menor · Menor pasa a Mayor · Justa se mantiene Justa · Disminuida pasa a Aumentada · Aumentada, a Disminuida |
Algunos ejemplos:
Segunda menor > Séptima mayor |
Cuarta justa > Quinta justa |
Tercera menor > Sexta mayor |
Cuarta disminuida > Quinta aumentada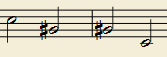 |
Inversión e intervalos complementarios
Se dice que dos intervalos son complementarios cuando ambos suman una octava. Tratándose de intervalos simples, al invertirlos siempre resulta su complementario. Por ejemplo, las quintas son complementarias de las cuartas, o las sextas menores son complementarias de las terceras mayores, etc.
También, los intervalos complementarios constituyen la distancia de una nota a otra, de forma ascendente y descendente, respectivamente. Por ejemplo, para llegar de “do” a “mi”, partiendo del do, tenemos que ascender una tercera mayor, o descender una sexta menor. Cada uno de estos intervalos son el resultado de invertir el otro, y son complementarios.
Todo esto nos ayuda a comprender e identificar mejor los intervalos.
Intervalos compuestos:
En el caso de intervalos compuesto, el proceso para su inversión es un poco más largo:
1º: Se reduce a intervalo simple
2º: Se hace la inversión de ese intervalo simple
3º: Se le amplía en tantas octavas como se le redujo
Y el resultado es el intervalo invertido.
Las transformaciones, en cuanto a su especie, son las mismas que en los simples (mayores pasan a menores, etc.). Y en cuanto al número, hay que realizar el proceso descrito antes, debiendo restar o sumar “7” cada vez que debamos reducir / ampliar una octava. En el ejemplo a continuación, vemos cómo una 10ª se convierte en 13ª, al invertir el intervalo siguiendo esos pasos:

1º: Transformamos la 10ª a intervalo simple, obteniendo una 3ª menor (10 – 7 = 3).
2º: Invertimos el intervalo simple, obteniendo una 6ª mayor.
3ª: Ampliamos el intervalo en tantas octavas como se le redujo, en este caso una, y obtenemos una 13ª (6 + 7 = 13).

esta muy bien para los examenes de pase de grado a profesional
podrías poner el ejemplo en clave de sol?
No es por ser quisquilloso, pero en la descripción de los pasos seguidos en el último ejemplo, me parece que no se obtiene una 3ª menor y luego una 6ª mayor, sino una 3ª mayor y una 6ª menor.
Hola, de “la” a “do” hay una 3ª menor, y de “do” a “la”, una 6ª mayor, no veo ningún error, un saludo!
No hay ningun error, de LA a DO está el semitono si-do, por lo tanto es una 3°m y las 3°m al invertirse da como resultado siempre una 6°M.
8=1 AA=DD
7=2 A=D
6=3 M=m
5=4 J=J
muchísimas gracias por la explicación y por esta lección si no fuera por personas como ustedes no tendríamos, yo en principio no podría estudiar solfeo.
Y una tercera aumentada en que se convierte al invertirlo?, gracias
En una sexta disminuida. Saludos!
Genial la explicación. Estoy muy agradecido.
Owwww gracias, estoy volviendo con esto asique debo ponerme en orbita, porque ésta aparte la tengo bastante olvidada.
Saludos!!!
Pregunta: si tengo fa agudo y un fa# más grave, eso es una octava aumentada, bien en consecuencia, Cómo hago la inversión?, que intervalo se obtiene?
Al invertirlo, la distancia entre ambas notas es de un semitono cromático. De fa a fa#, hay medio tono cromático. ¡Espero haberte ayudado!
esta muy interesante todo ando buscando aprender bien y entender todo bien
EN LAS TRANSFORMACIONES que hiciste, en la tabla
dice que una 4º a invertirse a 5º ……. pasa de menor a mayor
ACASO NO SON JUSTAS?
En la tabla dice que las justas se mantienen justas, las aumentadas a disminuidas y viceversa. Un saludo
hola una pregunta en la inversion ¿da igual que nota se ponga o tiene que tener relacion con alguna de las dos notas del intervalo antes de ser invertido?
Pon también con sostenidos y bemoles, que así o entiendo mejor. Me encanta tu página y la explicación, ahora me queda más claro.
No hay ningun error, de LA a DO está el semitono si-do, por lo tanto es una 3°m y las 3°m al invertirse da como resultado siempre una 6°M.
8=1 AA=DD
7=2 A=D
6=3 M=m
5=4 J=J
El intervalo invertido debe tener dirección contraria al no invertido, no? Además, el orden de las notas no debe cambiarse al invertir (cambia la altura)
HOLA, EXCELENTE PAGINA. FELICITACIONES¡¡¡
UNA DUDA :
SI DESDE DO A REb EXISTE UN NTERVALO DE SEGUNDA MENOR, COMO SE DENOMINARÍA UN INTERVALO ENTRE DO Y DO# ?
GRACIAS DE ANTEMANO ¡
Muy buen artículo y muy bien explicado, me ha set ido de mucho GRACIAS
Aún así tengo una pregunta:
Me piden invertir una Octavia de fa a fa sostenido el problema es que la inversión no me da unísono porque un fa y un fa sostenido no es un unísono
Que debo hacer?